计算机图形学（1）：感性认识

图源：《Magnet》Matcha_ 102235547

本系列笔记为结合了个人理解的非初学者向笔记，包括《CMU 15-462》、《Games 101：现代计算机图形学入门》、《Games 102：几何建模与处理》、《Introduction to 3D Game Programming with DirectX 12》等数个知识来源。

什么是计算机图形学

计算机图形学：利用计算机合成视觉信息或利用计算机合成/操控感官信息的学科。

计算机图形学的应用

• 影视
• 动画
• 游戏
• 数据可视化
• 工业设计，平面设计
• 数字绘画
• 虚拟现实
  • 虚拟现实（VR）：指所看到的一切均为虚拟的，比如虚拟现实游戏、虚拟现实视频等。
  • 增强现实（AR）：指看到的是真实的现实 + 虚拟的、对当前现实进行分析处理或修改等生成的虚拟事物，比如Apple ARkit。
  • 混合现实（MR）：VR + AR，使用类似VR的手段，达到AR这种结合当前现实与虚拟事物的效果，比如Hololens。
• 制造业（3D打印）
• 模拟与数字孪生
• 排版与字体设计
  • “The Quick Brown Fox Jumps Over The Lazy Dog”：一句有意义的英文句子，内含全部的26个英文字母，常用来对字体（字形、字号、间距等）进行测试。
  • “Lorem ipsum dolor sit amet, consectetur adipisicing elit.”：又叫“乱数假文”或者“哑元文本”。主要的目的为测试文章或文字在不同字型、版型下看起来的效果。更多资料请查阅：https://cn.lipsum.com/。

计算机图形学与计算机视觉的区别

• 计算机图形学：将数据转化为图形。也就是“画出来”。
• 计算机视觉：将图形转化为数据。也就是“看到”。

计算机图形学需要哪些基础

• 表示方法（编码）
• 采样与混叠
• 数学方法（表示三位物体和动作）
• 光线
• 透视

思考：展示一个正方体

• 如何表示
  • 顶点：利用坐标
  • 边：利用边的两个顶点唯一确定
• 如何绘制
  • 三维图形转化为二维图形：小孔成像模型
    • 设相机坐标为 $(a,b,c)$ ，待确定点的坐标为 $(x,y,z)$ 。要得到该点在二维平面上的坐标，可进行如下算法步骤：
    • 1. $(x,y,z)$ 与 $(a,b,c)$ 相减，得到原三维点与摄像机的相对位置；
    • 2. 将其中的 $(x,y)$ 与 $z$ 相除，得到 $(\frac{x}{z},\frac{y}{z})$，即是所求的 $(u,v)$。
  • 连线。这就要细说到电脑如何绘制直线。

重要问题：计算机怎么展示直线？

• 先得知道计算机怎么显示图像：“光栅显示器”。
• 特点：
  • 图像表示为由像素组成的二维网格。
  • 每个像素可拥有不同的颜色值。

光栅化

• 将连续的物体转换为离散的像素在光栅网格上的表示（即由栅格组成的图像）的过程。也即把顶点数据转换为片元的过程。

怎么光栅化？（简单讨论无粗细的直线）

• 直接的想法：只要原始的连续物体触及了某个像素，该像素就应该显示。缺点：误差大。
• 在部分图形API中的实现：菱形测试区域法。
  • 更多资料：https://docs.microsoft.com/zh-cn/windows/uwp/graphics-concepts/rasterization-rules
• 不一定是最优解：看需求。通过需求挑选不同的算法。
• 除了误差（锯齿），覆盖率也是衡量光栅化效果的重要指标之一。

怎么找到对应的栅格（像素）？

• 暴力方法：遍历每一个像素，判断是否满足显示要求，满足就点亮进行显示。缺点：速度极慢。
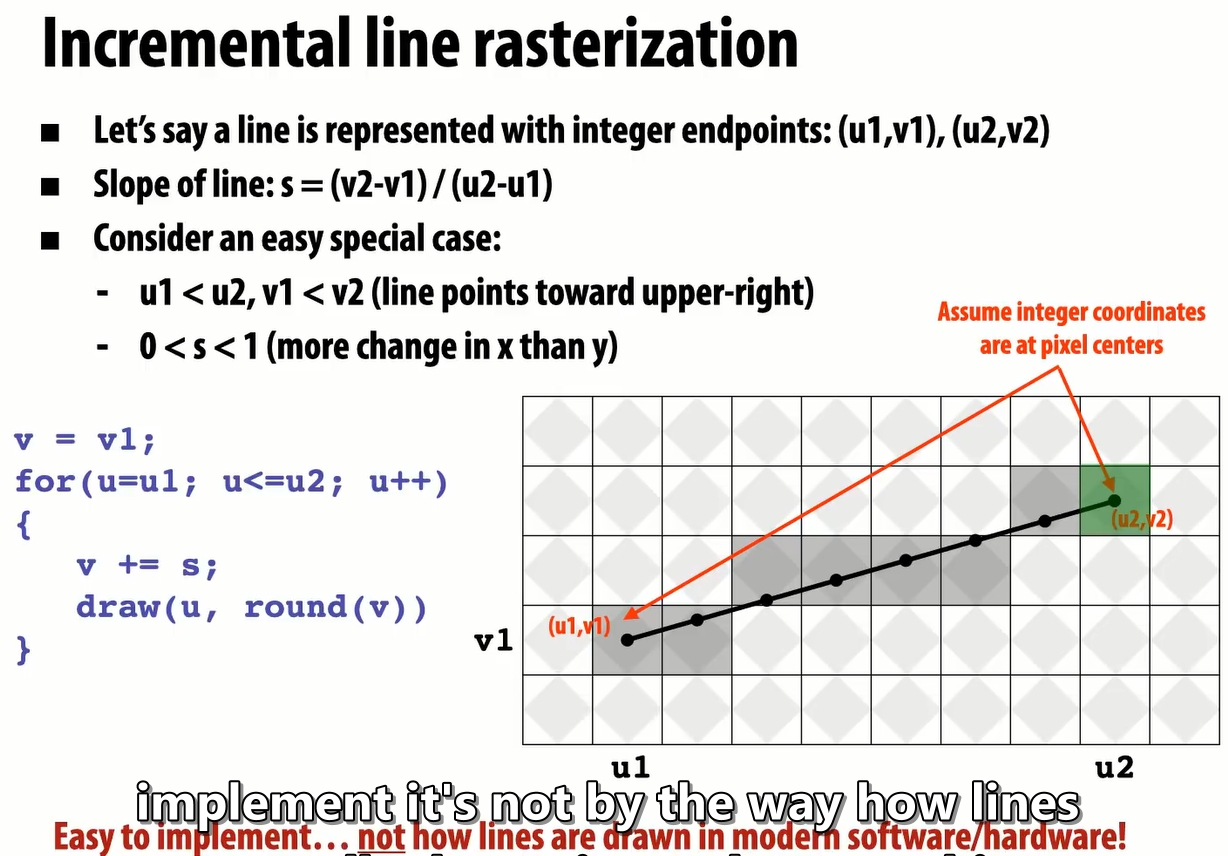
• “增值行光栅化”：简单的演示用自定义算法，利用直线的斜率，确定哪些像素用于显示。
  • 设有一直线，起点为$(u_1,v_1)$，终点为$(u_2,v_2)$。假设有$u_1 < u_2, v_1 < v_2$且$0<s<1$。可依据如下过程寻找像素（伪代码）：

p = (u, v);
v = v1;
for(u = u1; u <= u2; u++) {
    v += s;
    draw(u, round(v));
}

小结

以上是一个虽简单但完整的CG流程——从表示，到计算，到光栅化，再到显示。不过现实的CG环境要远远比这复杂。我们没有提到一些对图像（渲染）的真实感至关重要的知识和算法，譬如：

• 几何体，尤其是复杂几何体
• 材质，透明、半透明或不透明
• 光线，照明
• 摄像机
• 运动

四大应用领域

• 常见图形学API：OpenGL，（Vulkan），DirectX 11，（DirectX 12）
• 1.光栅化
  • 将几何基元投影至屏幕上，将投影后的几何基元拆分为“像素”
  • 现代OpenGL下的光栅化：https://vispy.org/getting_started/modern-gl.html
  • 透视投影与平行投影。
• 2.光线追踪
  • 从相机射出光线（采样视线）打到每个像素上。
  • 计算交叉（intersection）和遮挡（shading）。
  • 继续弹射（bounce）光线，直到回归光源
  • 参考：https://en.wikipedia.org/wiki/Ray_tracing_(graphics)。
• 曲线与网格（Mesh）
  • 计算机图形学中表示几何体的方法。
  • 贝塞尔曲线
  • Catmull-Clark细分曲面，参考https://blog.csdn.net/McQueen_LT/article/details/106102609
• 动画与模拟
  • 关键帧（K帧）动画
  • 弹簧质点（Mass Spring）系统模型，参见：https://blog.csdn.net/u011618339/article/details/106225426