D^3CTF 2021 - Misc - easyQuantum WriteUp
图源:@しぐれうい 《雨に恋う》 83975808
cap.pcapng用Wireshark打开,清晰可见TCP的三次握手和四次挥手:


于是需要仔细分析中间的数据传输过程。
注意到某些数据包内有“numpy”等字符串:
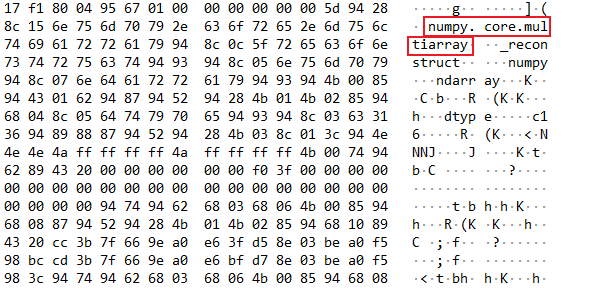
于是想到可能是某种兼容Python的序列化方法。
D^3CTF 2021 - Misc - easyQuantum WriteUp
图源:@しぐれうい 《雨に恋う》 83975808
cap.pcapng用Wireshark打开,清晰可见TCP的三次握手和四次挥手:


于是需要仔细分析中间的数据传输过程。
注意到某些数据包内有“numpy”等字符串:

于是想到可能是某种兼容Python的序列化方法。
图源:《希娜狄雅》爱东东不爱吃生肉 116447899
我又来随便糊一篇文章了。
题目设定如下:
An otaku used VeraCrypt to encrypt his favorites.
Password:
rctfFlag format:
rctf{a-zA-Z0-9_}
题目给的提示十分简单。于是准备 VeraCrypt,开始解题。
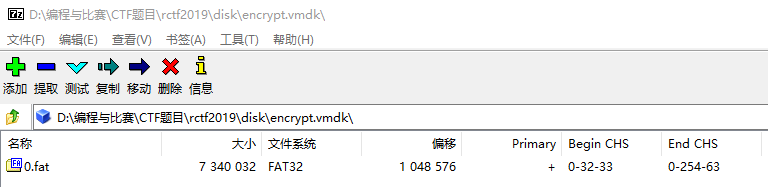
首先下载题目附件,得到 rctf-disk.zip,解压得到 encrypt.vmdk。因为无法确定 vmdk 是 VeraCrypt 加密完的虚拟硬盘文件随便改了个格式,还是存储了 VeraCrypt 加密后虚拟磁盘文件的虚拟磁盘(这话真的超级绕hhh),因此先尝试使用 7zip 打开该文件。
图源:《送别》 nitoo190 112680544
所以说,近期铺天盖地宣传的“西湖论剑”网络安全技能赛预选已经结束了。在这里随便糊一篇文章(也是我第一次写Write-Up文章),就聊聊杂项最先放出的那个第二题的解法。
首先拿到题,解压,发现里面有“题目描述”,先看描述,是这么写的:
我们截获了一些IP数据报,发现报文头中的TTL值特别可疑,怀疑是通信方嵌入了数据到TTL,我们将这些TTL值提取了出来,你能看出什么端倪吗?
然后看给出的另一个文件,ttl.txt,里面的内容是这样的:
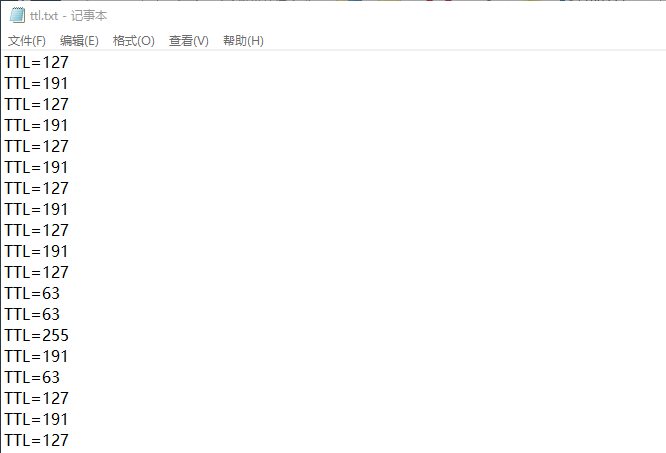
不难发现TTL值只有 $63$,$127$,$191$,$255$ 四种,都是$2$的某次幂$-1$的值。于是将这四个数都转换成二进制,得到 $111111_2$、$1111111_2$、$10111111_2$、$11111111_2$ 四个二进制数。从后面两个数字可以观察到二进制数的开头两位似乎有关系。又因为TTL值为一个8位整数,进行合理猜想,不妨将不足8位的二进制数开头补0,变为8位后再取开头两位。即:$00111111_2$、$01111111_2$、$10111111_2$、$11111111_2$提取开头两位为:$00_2$、$01_2$、$10_2$、$11_2$,恰好为全排列,可以用于数据的存储。
D^3CTF 2021 - Misc - Robust WriteUp
图源:@電瘋扇 《仓鼠松鼠》 91999586
“Robust”意为“鲁棒性”。
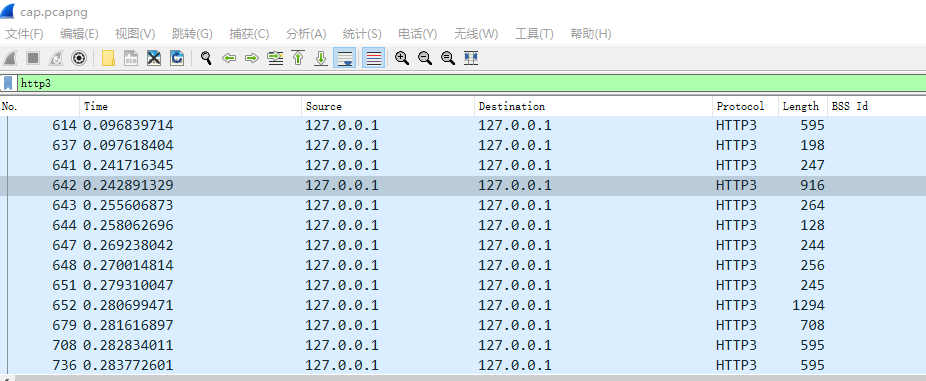
打开cap.pcapng,发现都是QUIC协议的数据包。结合提供的firefox.log(即使用firefox浏览器访问时生成的SSL Key Log)可以想到基于QUIC协议且强制使用TLS 1.3的HTTP3。
导入SSL Key Log:
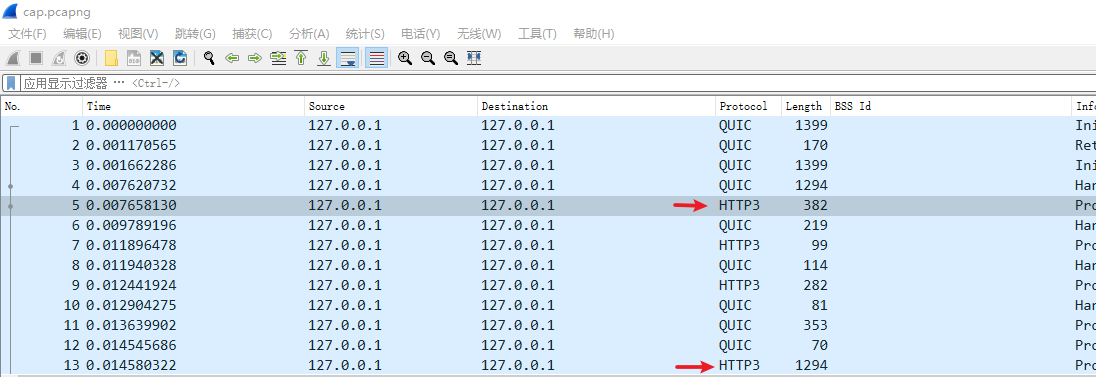
清晰可见HTTP3数据包。利用过滤器过滤出所有HTTP3数据包,然后从头查看:
1 | http3 |
Update your browser to view this website correctly.&npsb;Update my browser now